The project Fate or Future of Tidal flats was a collaboration between TU Delft and SKLEC, the State Key Laboratory for Estuaries and Coasts of the East China Normal University in Shanghai. The PhDs Cynthia Maan and Qin Zhu worked in this project and defended their thesis successfully, see links for their theses and papers.
The project resulted in a insights in the developement of tidal flats. Cynthia Maan developed numerical models and explored the feedback mechanisms. Qin Zhu carried out field experiments in the Netherlands and China, unravelling the mechanisms of erosion of tidal flats.
Zhu, Q. (2017). Sediment dynamics on intertidal mudflats: A study based on in situ measurements and numerical modelling.
Maan, D.C. (2019). Long-term Dynamics and Stabilization of Intertidal flats: A system approach.

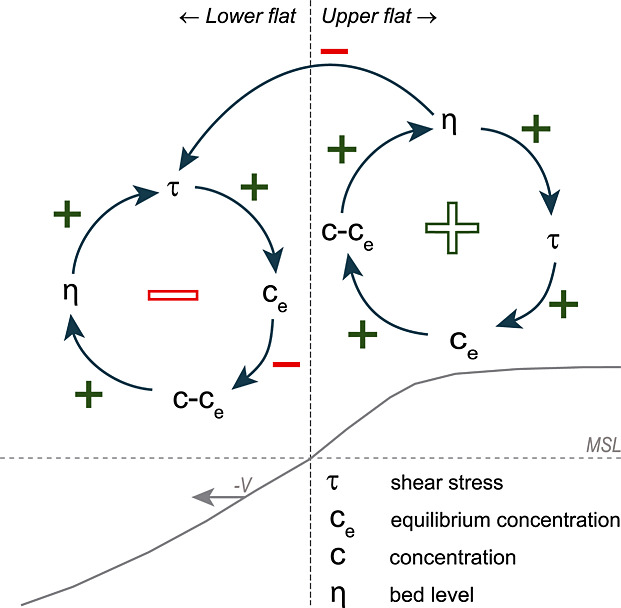
Feedback loops on a “tide controlled” flat. The arrows with positive and negative signs indicate positive and negative influences inbetween the parameters, respectively. An uneven number of negative influences within a loop results in a balancing feedback loop, whereas an even number of negative influences within a loop results in a reinforcing feedback loop. The bed level on the lower flat is controlled by a balancing feedback loop, i.e., if the deposition flux is initially larger than the erosion flux, i.e., c − ce>0, net sedimentation occurs and the bed level rises, resulting in locally larger tidal flow velocities and shear stresses, which diminish the initial imbalance. The bed level on the higher flat is controlled by a reinforcing feedback loop; an initial imbalance is amplified, because a rise (decay) in the bed level results in smaller (larger) tidal flow velocities and smaller (larger) shear stresses on the bed. At the same time, a rising upper flat reduces the tidal flow and shear stresses on the lower flat (indicated by the arrow with negative sign inbetween the loops), resulting in a migration of the whole flat.
